高速多重極境界要素法による大規模電磁場・弾性場解析
Large scale analysis of electromagnetics and elasticity with fast multipole boundary element method

概要

偏微分方程式の数値解法として古くから知られる境界要素法（BEM) は、電磁場、弾性場解析の数値計算において大変有効な解法であることが知られている。特に、解析対象物体の境界だけをメッシュ分割すればよいという著しい特徴を有しているため、無限遠方を含むような波動散乱問題の解析には大変有利である。さらに、高速多重極法（FMM)という高速アルゴリズムを用いることにより、特に大規模問題において、有限要素法や差分法といった領域型解法よりも高速に、かつ少ないメモリで解析できると考えられている。

本グループではこれまで、弾性場、電磁場解析における高速多重極法の開発を行ってきた。例えば、ラプラス方程式において１億自由度、弾性問題において3000万自由度という超大規模問題を解いた実績がある。また、近年、フォトニック結晶等の新しい光学材料の開発に伴って波動周期境界値問題の重要性が高まっているが、大規模問題を取り扱うことのできる解析手法が存在しなかった。そこで、波動周期境界値問題を対象とした周期高速多重極法の開発を行い、大規模解析への道を開いた。図に数値解析例を示す。

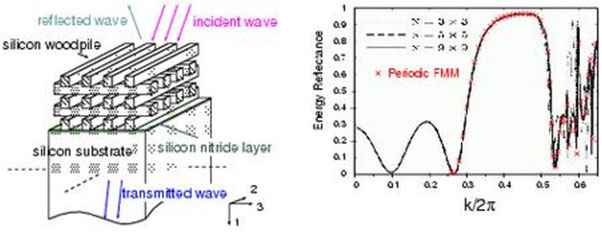
図：（左図）周期ウッドパイル構造、（右図）周期ウッドパイル構造における、波数に対するエネルギー反射率（×印：周期多重極法による結果、黒実線：Gralak et al. (2003)による結果）

産業界への展開例・適用分野

近年着目されているフォトニック結晶やメタマテリアルといった新しい光学材料は周期構造を有している。また光学機器には周期境界値問題（やその変形）としてのモデル化が可能なものが多い。一般にこれらの材料・素子・機器等は複雑な形状をしていることが多いため、これを対象に数値解析を行う場合にはしばしば大規模問題に帰着される。このような問題には、周期高速多重極法による解析が大変有効であると考えられる。現在、種々の光学の問題における実用化をにらんだ数値解析手法の研究・開発を進めている。

研究者

氏名	専攻	研究室	役職（学年）
西村　直志	複雑系科学	西村研究室	教授
大谷　佳広	複雑系科学	西村研究室	講師

Website

---