周期外力下の粉粒体の数値解析
Numerical analysis of periodically forced granular materials

概要

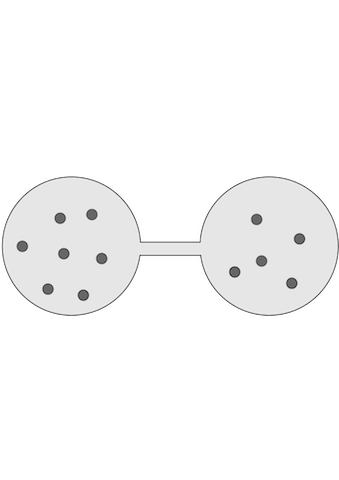
容器の底に等分する仕切りを設け、両室に粉粒体を入れ、鉛直方向に加振する。強く加振すると、粉粒体は仕切りを自由に飛び越え、両室の粒子数密度は等しくなる。加振強度を適当な値に設定し、両室の粉粒体の数が等しい状態から加振すると、粉粒体は片方の部屋に凝集する。粉粒体の数密度が僅かに偏ると、衝突間平均移動距離は数密度の大きい部屋では小さくなり、数密度の小さい部屋では大きくなる。その結果、数密度の偏りは更に増大し、凝集が起こる。このような現象が水平加振でも起こることを数値解析により示す。この水平加振の状況は1955年のHodgkin-Keynesのイオンチャネルのモデルとよく似ている。二室をパイプのようなもので繋ぎ、水平加振を施すと、平均二乗変位が時間の平方根に比例する遅い異常拡散と時間に比例する通常の拡散のクロスオーバーが生じるとの先行研究がある。そのようなクロスオーバーは結合カオス系の完全カオス同期が僅かに破れて生じたオンオフ拡散においても観測される。オンオフ拡散と上記のイオンチャネルモデルとの関連についても研究する。

産業界への展開例・適用分野

粉粒体の数値解析には、離散要素法(Discrete Element Method, DEM)という粉体工学や土木工学で広く使われている手法を用いている。この手法の応用例は、液状化や土石流の地盤の挙動解析、リチウムイオン電池のイオンやコピー機等のトナーの解析など枚挙にいとまがない。

研究者

氏名	専攻	研究室	役職/学年
宇都宮 将人	先端数理科学専攻	非線形物理学講座	その他学生

---