終端制約付き非線形最適制御問題に対する代数的アプローチ

概要

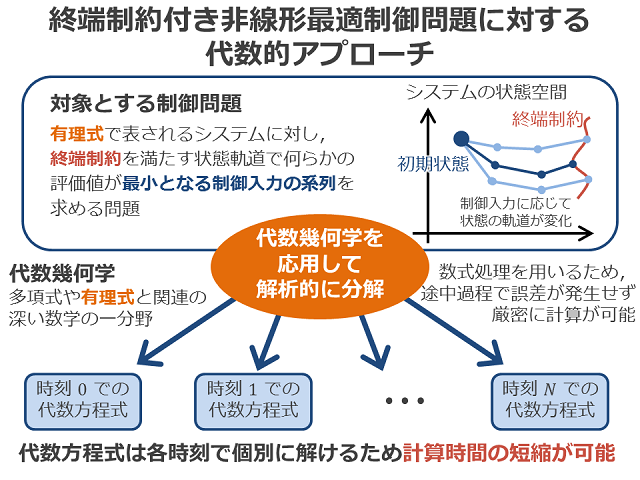
非線形システムに対し、何らかの評価関数を最小化する制御入力を求める問題を非線形最適制御問題という。モデル予測制御はこの問題を繰り返し解く制御手法であり、最適制御問題にある種の終端制約を課すことで、安定性を保証することが可能である。しかしながら、計算コストが大きく実現が難しいという課題があった。本研究では、制御対象のシステムが有理式で表される場合の終端制約付き最適制御問題に着目し、代数幾何学と呼ばれる多項式や有理式と関連の深い数学の一分野を応用する。これにより、解くべき最適制御問題を複数の比較的小さな代数方程式の集合へと数式処理を用いて分解することが可能となり、計算コストの削減が可能となる。

産業界への展開例・適用分野

本研究の手法は、磁気浮上系やセミアクティブダンパなど、ダイナミクスが有理式または多項式で記述される系に対して適用可能である。また、テイラー近似やパデ近似などを用いることで、三角関数を含むロボットアームなどのより一般的な非線形システムに対しても適用可能であると考えられる。これにより、従来は計算コストの問題が存在していた非線形システムに対し、非線形モデル予測制御を適用し、安定性を保証することができる。

研究者

氏名	専攻	研究室	役職/学年
庵 智幸	システム科学専攻	大塚研究室	修士2回生
河野 佑	その他所属	フローニンゲン大学	研究員
大塚 敏之	システム科学専攻	大塚研究室	教授

---