超高速カオスモンテカルロ計算の最適戦略について
Optimal Strategy of Superefficient Chaotic Monte Carlo Computation
概要
カオスを用いた汎用のモンテカルロ計算を提案し、通常の誤差分散が計算時間Nに対して逆比例するのに対して、Nの自乗に逆比例するSuperefficientなモンテカルロ法を発見し提案していた。
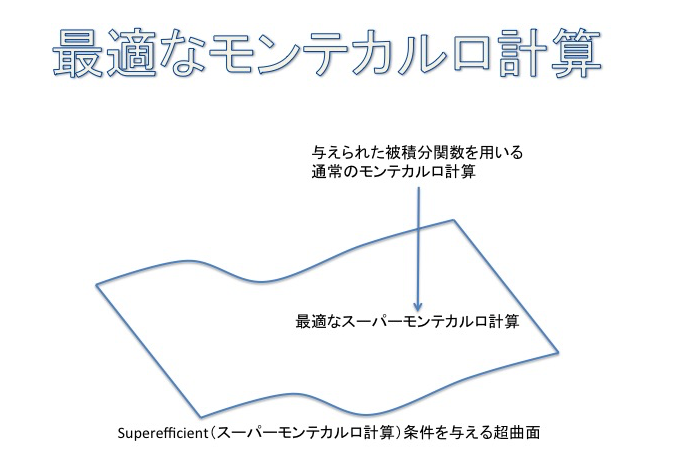
本研究は、そのSuperefficientなモンテカルロ法のクラスの中での最適化アルゴリズムを、乱数生成器として用いるカオス力学系の不変測度μ(dx)に関する自乗可積分関数の集合からなるヒルベルト空間の射影演算子を用いることにより構成した。具体的には, ヒルベルト空間上でSuperefficiency条件を満足する空間(拡散係数=0)への直交射影を行った先が最適なSuperefficientなモンテカルロ計算に相当する。
産業界への展開例・適用分野
本研究はマルコフチェインモンテカルロ(MCMC)法のマルコフ性を、決定論的カオスに置き換え、最適化したものであることから、MCMC法が適用される機械学習をはじめ、従来のLSI半導体回路最適化設計シミュレーション、デバイスノイズの影響を考慮したシミュレーション、金融保険分野におけるリスク評価、オプション価格の評価など多岐に渡る分野での高速化が期待できる。また本手法は、カオスがべき分布を有する確率分布も効率的に生成できることが解っているため、べき分布を特徴とする機械学習、モンテカルロ計算の高速化にも適用可能である。
研究者
| 氏名 | 専攻 | 研究室 | 役職/学年 |
|---|---|---|---|
| 梅野 健 | 数理工学専攻 | 物理統計学 | 教授 |