時間の矢は存在するのか
Is there the Time's Arrow?
概要
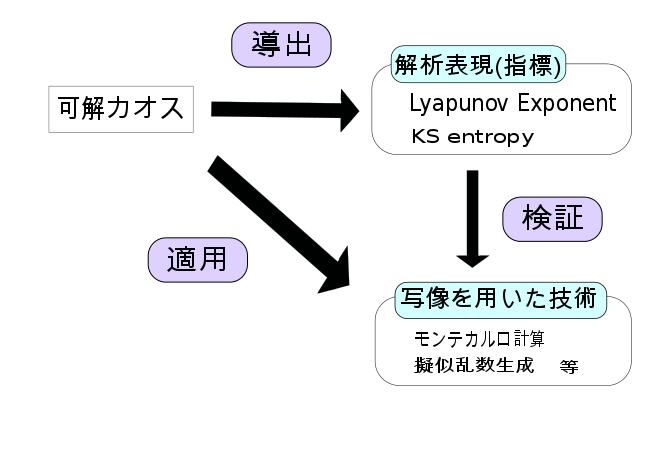
本発表ではシンプレクティック写像において発生する可解カオスについて述べる. 可解カオスとは写像の不変密度関数の解析表示がわかっているカオスである. この性質を利用して, 写像のエルゴード性を証明し, Lyapunov指数の解析解を求めることができた. さらに, Pesinの等式を用いて, Kolmogorov-Sinai(以下KSエントロピー)の解析表示を導出することができた. KSエントロピーは未来を予想するのに不足する情報量を表す. さらに, SKエントロピーは粗視化のエントロピーにおいて精度を極限に取った場合の時間微分に相当する. よって, KSエントロピーが正であることから, エントロピーの時間微分が正であることがわかる.
産業界への展開例・適用分野
KSエントロピーは未来を予測するのに不足する情報量を表す. そこで, この写像を用いれば, モンテカルロ計算や擬似乱数生成等写像を応用する技術を解析的に評価することができると考えられる.
研究者
| 氏名 | 専攻 | 研究室 | 役職/学年 |
|---|---|---|---|
| 大久保 健一 | 数理工学専攻 | 物理統計学 | 博士1回生 |
| 梅野 健 | 数理工学専攻 | 物理統計学 | 教授 |