近年,マイクロ流体デバイスやマイクロマシンの動作原理として,熱的に駆動される流れが注目されている.マイクロ系の流体では温度差によって流れが形成されることが知られており,レーザー光などを用いて流体やその周囲の物体を局所的に加熱することで,熱的に流れを駆動することができる.光が熱へ,そこからさらに流体の流れや物体の動きへと変換される現象の発見は,今から100 年以上も前の Crookes のラジオメーター(※1)にまで遡るものの,熱と流れの関係はいまだ明らかになっていないところも多い.ラジオメーターの羽のような,尖った物体まわりの流れの振舞いはその一例である.この困難さの主な原因は,マイクロ気体の振舞いが従来の流体力学の枠組みで記述できないところにある.このため数値シミュレーションを行う際には,流れや圧力だけを計算する通常の数値流体力学とは違い,気体分子の速度分布関数,すなわち「どの速度をもつ気体分子がどこにどれくらいいるか」まで計算しなければいけない.そしてそれには,Boltzmann 方程式と呼ばれる複雑な微分積分方程式の解を計算する必要がある.本研究では,円板まわりの3次元流れについて,Boltzmann 型方程式に対する数値計算スキームを方程式の積分形に基づいて構成し,本学のスーパーコンピュータを用いて実装した.数千個のコアと数 TB のメモリを用いた並列コンピューティングによる数値計算を実行し,円板まわりの気体の振舞いを速度分布関数のレベルで得ることに成功した.その結果から,速度分布関数の不連続の振舞いが数値的に明らかになったほか,気体分子の平均自由行程(※2)の変化に対して流れや圧力が特異的に振舞う領域が,円板の尖端近傍に見出された.
※1 ガラス容器の中に羽根車が取り付けられた装置.容器内の気体はやや低圧に保たれており,羽の片面だけが黒く塗られている.装置に光を当てると,黒塗りの面がもう一方の面に対して高温になることによって流れが誘起される.その流れの反力が羽にはたらくことで羽根車が勢いよく回り出す.
※2 気体分子が連続する2回の分子間衝突の間に進む距離の平均を平均自由行程と呼ぶ.
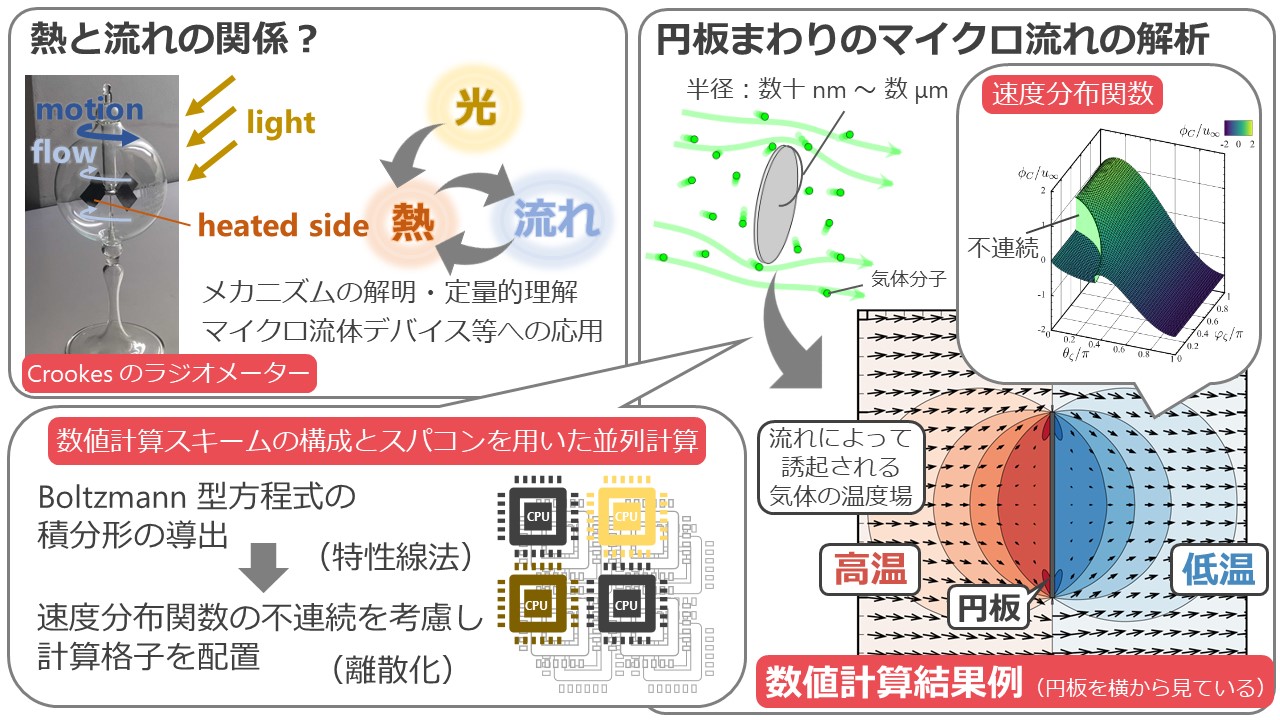
熱と流れの間の関係を明らかにすることは,マイクロ流体デバイス・マイクロマシンの基盤技術の発展につながる.特に,Boltzmann 方程式の数値的および数理的な解析を通して,流れや動きの制御技術への応用へ向けた基礎的な理解が得られる.一方で,本研究で提案する数値計算スキームは,マイクロ気体流れだけにとどまらず,Boltzmann 型方程式でモデル化される他の現象(電磁波(光)の放射輸送,バクテリアの集団挙動など)のコンピュータシミュレーションにも応用できる.
| 氏名 | コース | 研究室 | 役職/学年 |
|---|---|---|---|
| 富田卓磨 | 先端数理科学コース | 応用数理科学分野 | 博士1回生 |
| 田口智清 | 先端数理科学コース | 応用数理科学分野 | 教授 |
| 辻徹郎 | 先端数理科学コース | 応用数理科学分野 | 准教授 |