近年注目を集めているマイクロ工学やエアロゾル工学などで問題となる微小な系では,熱遷移流と呼ばれる現象(温度勾配によって駆動される気体の流れ)に代表されるような,我々の身近にある気体では見られない現象が起こる.実はこのような現象は従来のマクロな流体力学では説明できないのだが,そこで必要となるのが分子気体力学である.分子気体力学の基礎方程式であるボルツマン方程式は,通常の流体力学が扱うような構成分子同士の衝突が頻繁に起こる気体から,分子同士の衝突が全く起こらない気体(自由分子流)まで,様々な気体の振舞いを記述できる.さて,ボルツマン方程式は複雑な微積分方程式であるため直接解を求めるのは通常困難で,数値的に解かれることが多い.しかし,微分方程式の主要な解法の一つである漸近解析がボルツマン方程式にも適用することができる場合があり,そのとき解を近似的に求めることができる.実は先ほど述べた「構成分子同士の衝突が頻繁に起こる気体」の場合には,漸近解析によって流体力学の基礎方程式であるナビエ・ストークス方程式とよく似た方程式(流体力学的方程式)をボルツマン方程式から導くことができる.この流体力学的方程式はボルツマン方程式よりも容易に解くことができ,気体の流速や温度などの情報を得ることができる.本研究では,ボルツマン方程式の漸近解析の適用例として,一様な気体流の中に置かれている球の周りに生じる流れを紹介する.その際,流体力学の文脈で起こる現象に加え分子気体力学特有の現象が生じることも併せて紹介する.
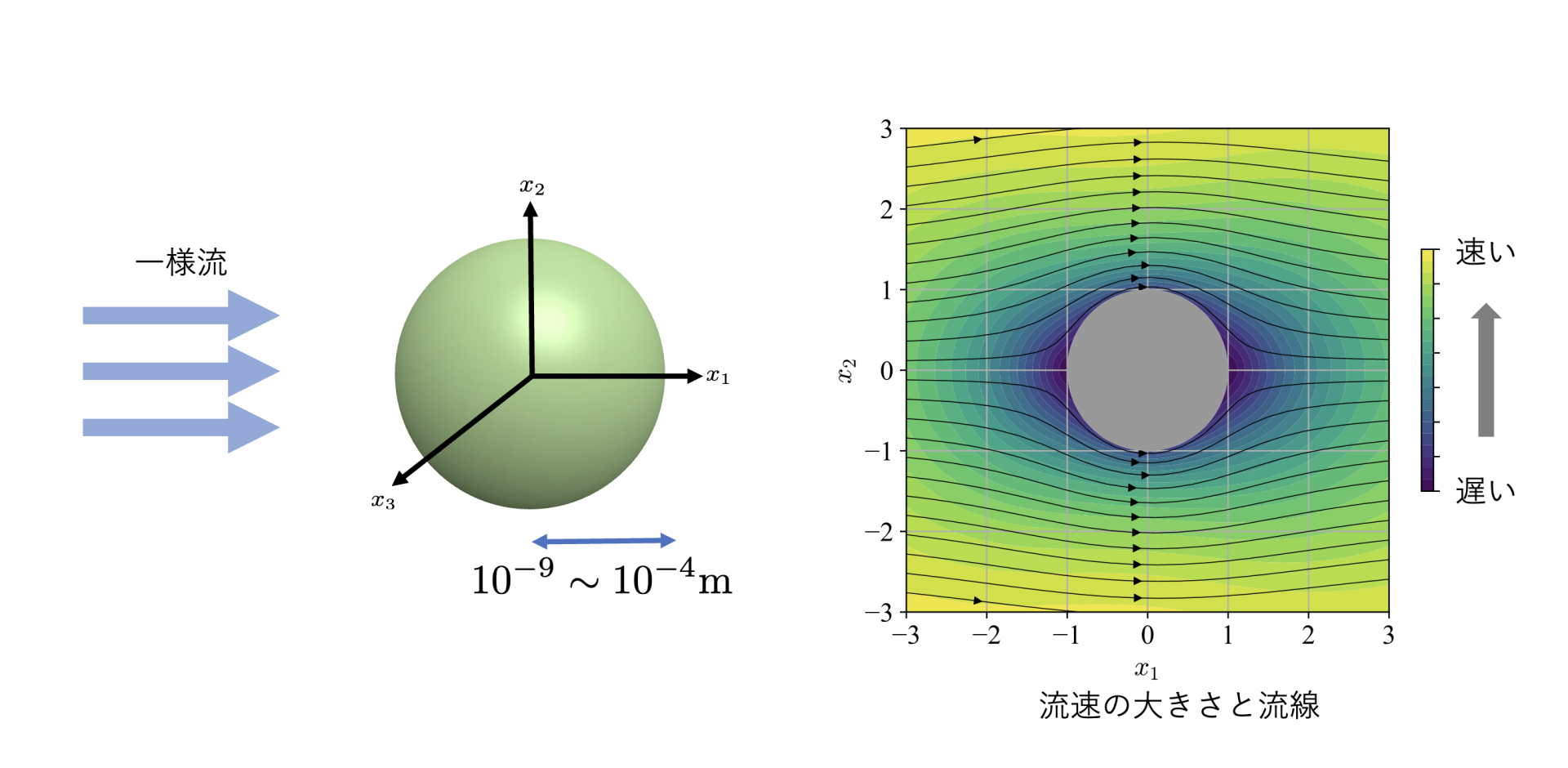
マイクロスケールの流れの中に置かれたセンサーなど、物体の周りの気体の振舞いの解析に応用できる.
| 氏名 | コース | 研究室 | 役職/学年 |
|---|---|---|---|
| 龍溪優希 | 先端数理科学コース | 応用数理科学分野 | 修士2回生 |
| 田口智清 | 先端数理科学コース | 応用数理科学分野 | 教授 |
| 辻徹郎 | 先端数理科学コース | 応用数理科学分野 | 准教授 |