This study covers the stochastic model predictive control (SMPC) of linear discrete-time systems subject to chance constraints. The stochastic optimal control problem is reformulated in a dynamic programming fashion to obtain a closed-loop performance and is solved using the interior-point method combined with a Riccati-based approach. The proposed method eliminates active sets in conventional explicit model predictive control and does not suffer from the curse of dimensionality because it finds the value function and feedback policy only for a given initial state using the interior-point method. The numerical experiment shows that the proposed method achieves a less conservative performance with a low computational complexity compared to existing methods.
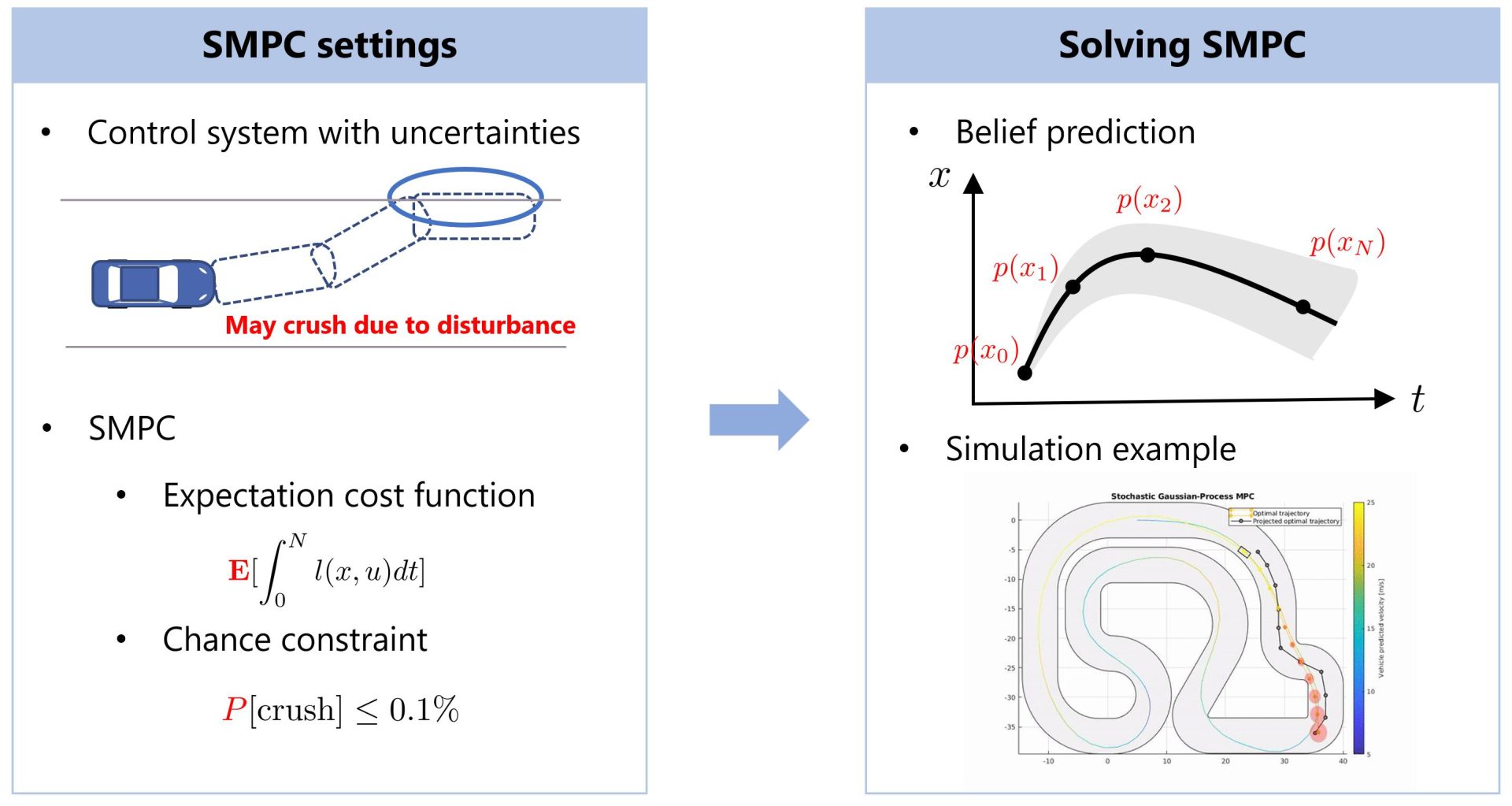
This algorithm can be applied into wide range of stochastic systems, for example, chemical system, energy system, robot system and so on.
| 氏名 | 専攻 | 研究室 | 役職/学年 |
|---|---|---|---|
| Jingyu Zhang | システム科学専攻 | 統合動的システム論分野 | 博士3回生 |
| 大塚敏之 | システム科学専攻 | 統合動的システム論分野 | 教授 |