遷音速ポテンシャル流の定常問題は、支配方程式が混合型の準線型偏微分方程式により記述される。この方程式はhodograph変換の適用により速度変数に対して線型偏微分方程式であるChaplygin方程式が得られる。Chaplygin方程式は変数分離による特解系がよく知られている。この特解は、単独ではhodograph逆変換のJacobianが退化する極限線が発生し物理的に可能な流れとならない。そのため、特解系の重ね合わせによってJacobianの退化を解消することを試みる。
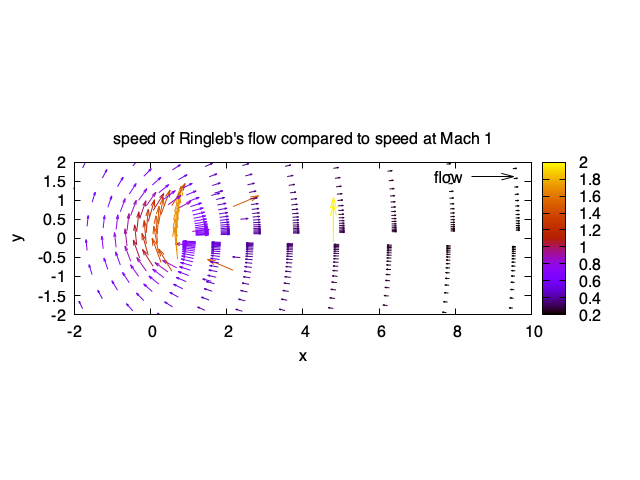
航空分野においてhodograph理論を用いて衝撃波の強さを最小限に抑える翼の設計がなされることがある。ポテンシャル流は1変数によって記述できることから計算負荷の軽減が期待できる。そのため、反復計算の時間を軽減するサロゲートモデルとしての活用も期待できる。
| 氏名 | 専攻 | 研究室 | 役職/学年 |
|---|---|---|---|
| 高橋 幸聖 | 先端数理科学専攻 | 応用解析学講座 | 博士2回生 |