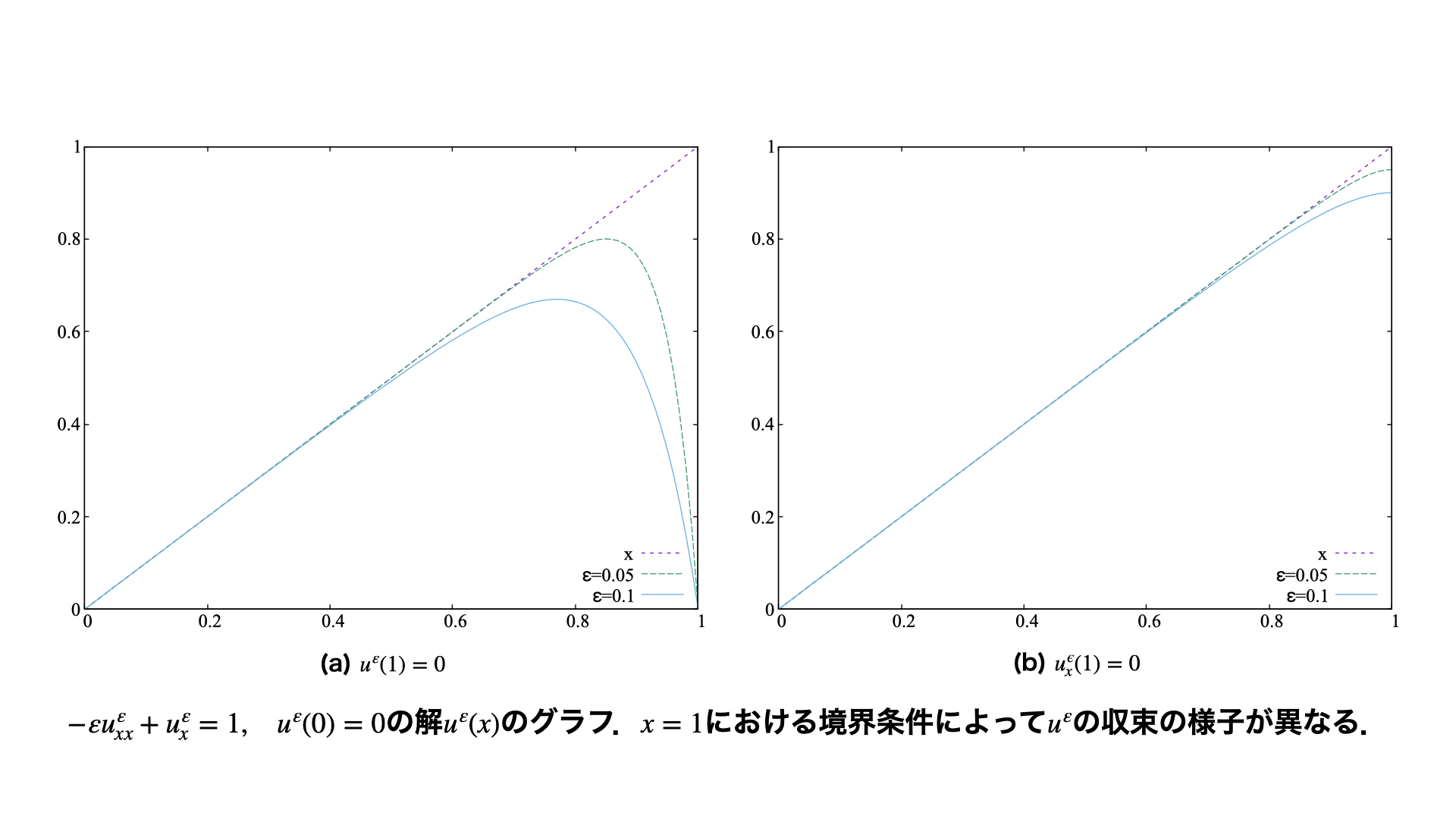
気体力学をはじめとした保存則を伴う現象の記述には1階双曲型偏微分方程式が用いられる.この方程式の解析には,粘性消滅法がしばしば用いられる.粘性消滅法とは,元の方程式に粘性項を付加することで得られる近似方程式の解に対して,粘性係数を0に近づける極限を取ることで元の解を構成する手法である.これは極限操作において方程式の階数が退化する特異摂動問題の一例であり,特に境界条件を伴う問題設定においては境界層の出現に起因して解析に困難が生じる.一方で,数値解析の観点から見れば粘性消滅法は一種の安定化手法であり,高精度な数値計算の実行のためには定量的な収束評価を得ることが重要である.そこで本研究では,特異摂動解の収束率と境界条件の関係を明らかとすることを目的として,線型移流方程式の定常問題を対象に収束率の定量的な評価を与えた.
流体力学,数値シミュレーション
| 氏名 | 専攻 | 研究室 | 役職/学年 |
|---|---|---|---|
| 今川真城 | 先端数理科学専攻 | 応用解析学講座 | 博士1回生 |
| 川越大輔 | 先端数理科学専攻 | 応用解析学講座 | 助教 |