従来の平均分散ポートフォリオでは, 期待値と分散によって投資家の意思決定水準が特徴づけれている. しかしながら, 実際の市場システムは複雑で様々な不均一性が存在するため, 従来手法によるリスク管理とポートフォリオ選択は適切ではないといった問題がある. 本研究では, 投資家の意思決定水準を非線形システムの観点から捉え, フラクタル解析手法の一種であるMFCCAとそれを基に定義される相互相関関数をポートフォリオリスクとして代用することで, 従来手法を拡張したmean-MFCCAアプローチを提案する.
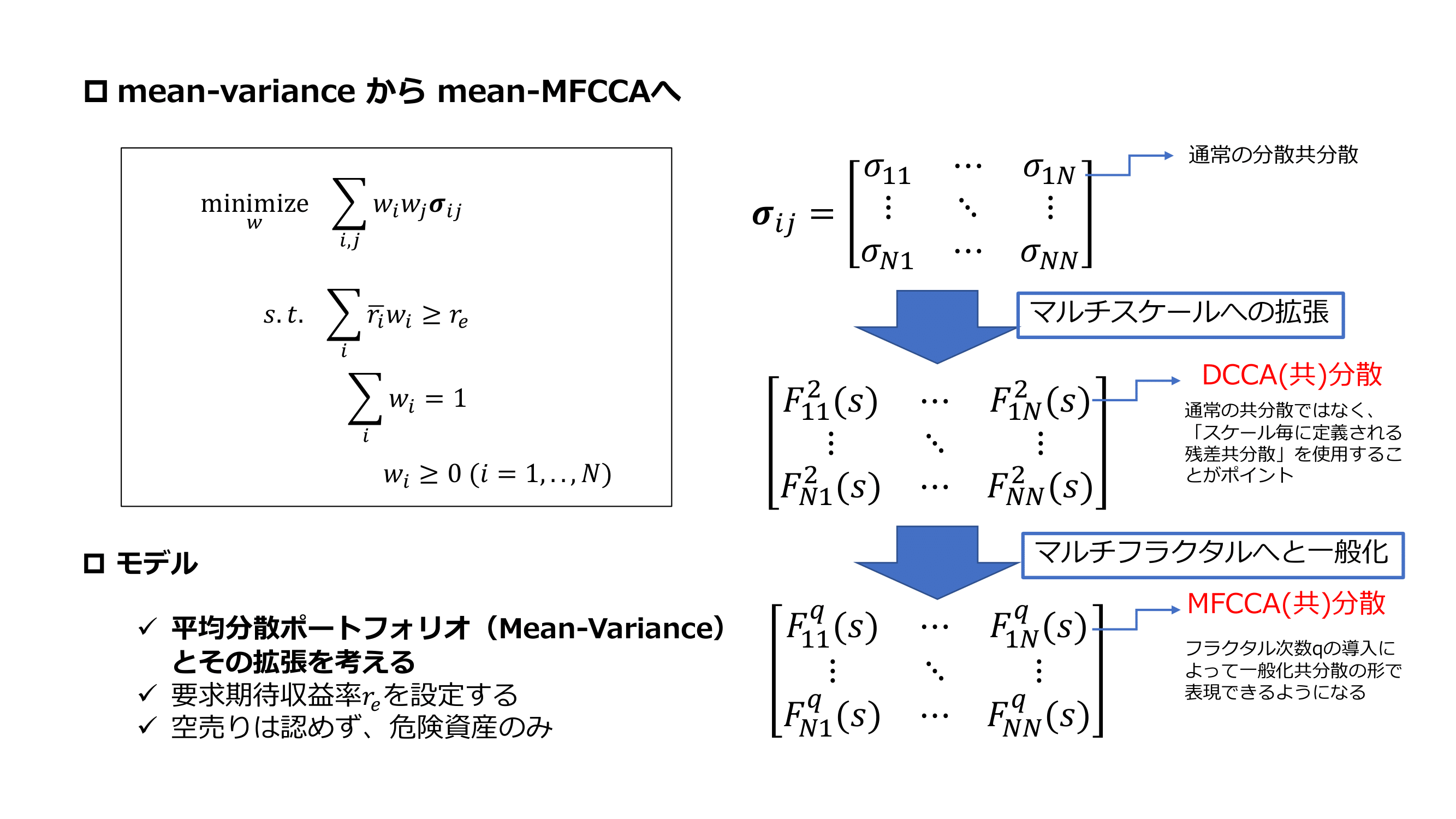
異なるスケール毎, すなわち投資ホライゾン違いを反映させた柔軟な配分選択が行えるため, 分散効果の高いポートフォリオが実現できるようになる. 実践的なリスク管理・ポートフォリオ戦略への適用が期待される.
| 氏名 | 専攻 | 研究室 | 役職/学年 |
|---|---|---|---|
| 柿中 晋治 | 数理工学専攻 | 物理統計学分野 | 博士3回生 |
| 梅野 健 | 数理工学専攻 | 物理統計学分野 | 教授 |