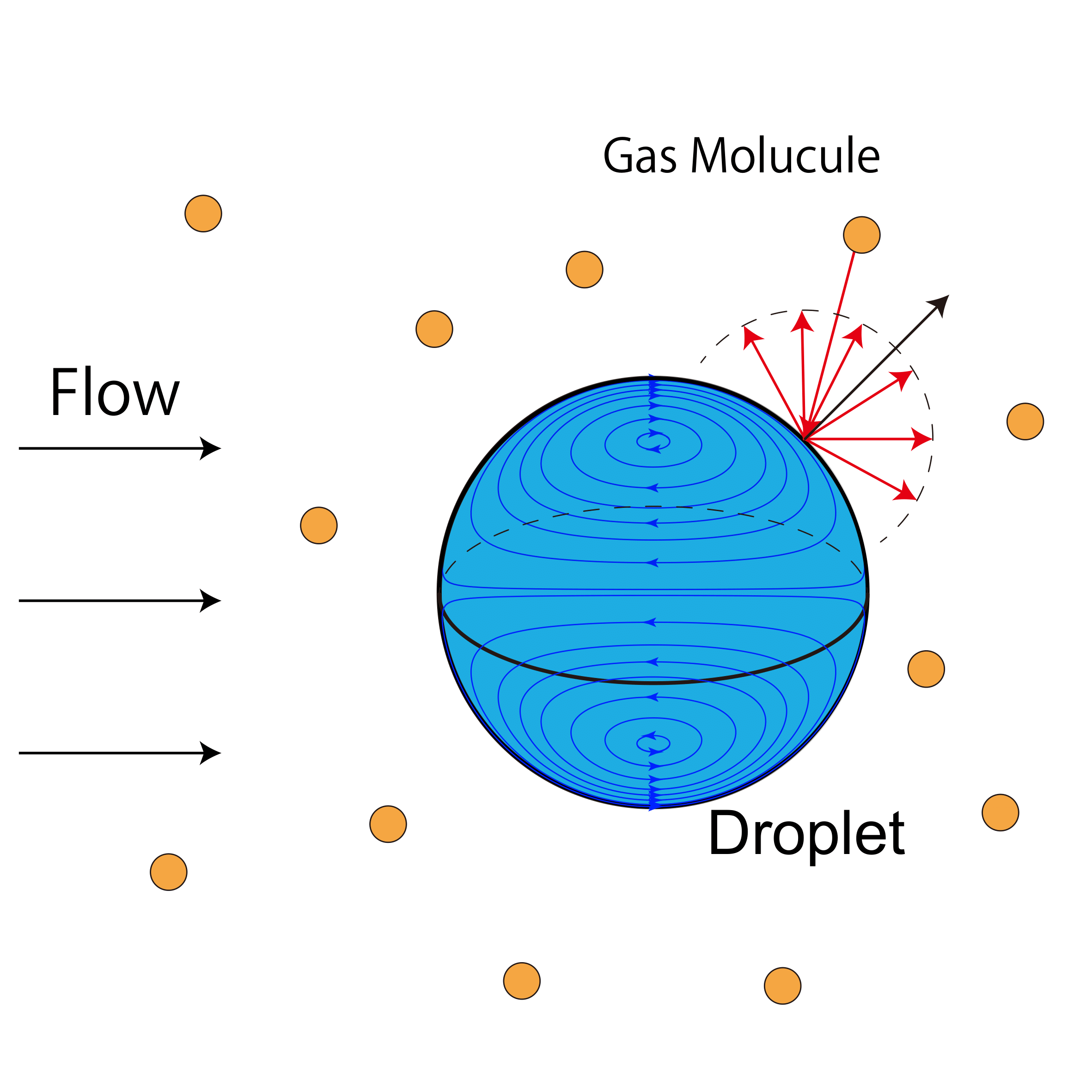
系の代表長さに対して分子の平均自由行程が無視できないとき、気体は希薄気体と呼ばれる。例えば、大気中に浮遊するエアロゾル粒子は代表長さである直径が小さいため、その周囲気体は希薄気体となる場合がある。希薄気体中の微小粒子まわりの流れや粒子に働く抗力を調べる研究は、大気中のエアロゾルの挙動や雲の生成にも関連する重要な基礎研究である。しかし希薄気体の振る舞いは、Boltzmann 方程式と呼ばれる複雑な微分積分方程式に支配されるため、その解析は十分に進んでいない。本研究では、一様な流れを持つ希薄気体中に球状液滴が置かれている問題を考える。球状液滴に働く抵抗や球まわりの流れを、線形化 Boltzmann 方程式と拡散反射境界条件によって調べ、定常状態において、希薄度が小さい場合の理論的な結果と、中程度の希薄度を持つ場合の数値計算結果について報告する。
微小粒子に働く抗力の詳細を明らかにすることで、エアロゾル感染の分析・予防や、天気予報の精度向上等の気象情報への寄与が考えられる。また、分子流体力学としては、低圧気体を扱う航空宇宙業界や真空装置、あるいは微小スケールを扱うマイクロ・ナノデバイス等への応用が考えられる。
| 氏名 | 専攻 | 研究室 | 役職/学年 |
|---|---|---|---|
| 松原湧汰 | 先端数理科学専攻 | 応用数理科学分野 | 修士1回生 |
| 田口智清 | 先端数理科学専攻 | 応用数理科学分野 | 教授 |
| 辻徹郎 | 先端数理科学専攻 | 応用数理科学分野 | 助教 |