平面円制限3体問題は地球と月の間を動くロケットの軌道設計や, 太陽と木星の間を運動する小惑星の運動を示すモデルとして知られている. ここでは,平面円制限3体問題を変分問題として考える.具体的には,6つの境界条件を考え, 各々の境界条件のもとで得られる汎関数の最小点から正則な周期解を構成できる十分条件を示す. また,得られた周期解がどのような形状をなしているかについて考察する.
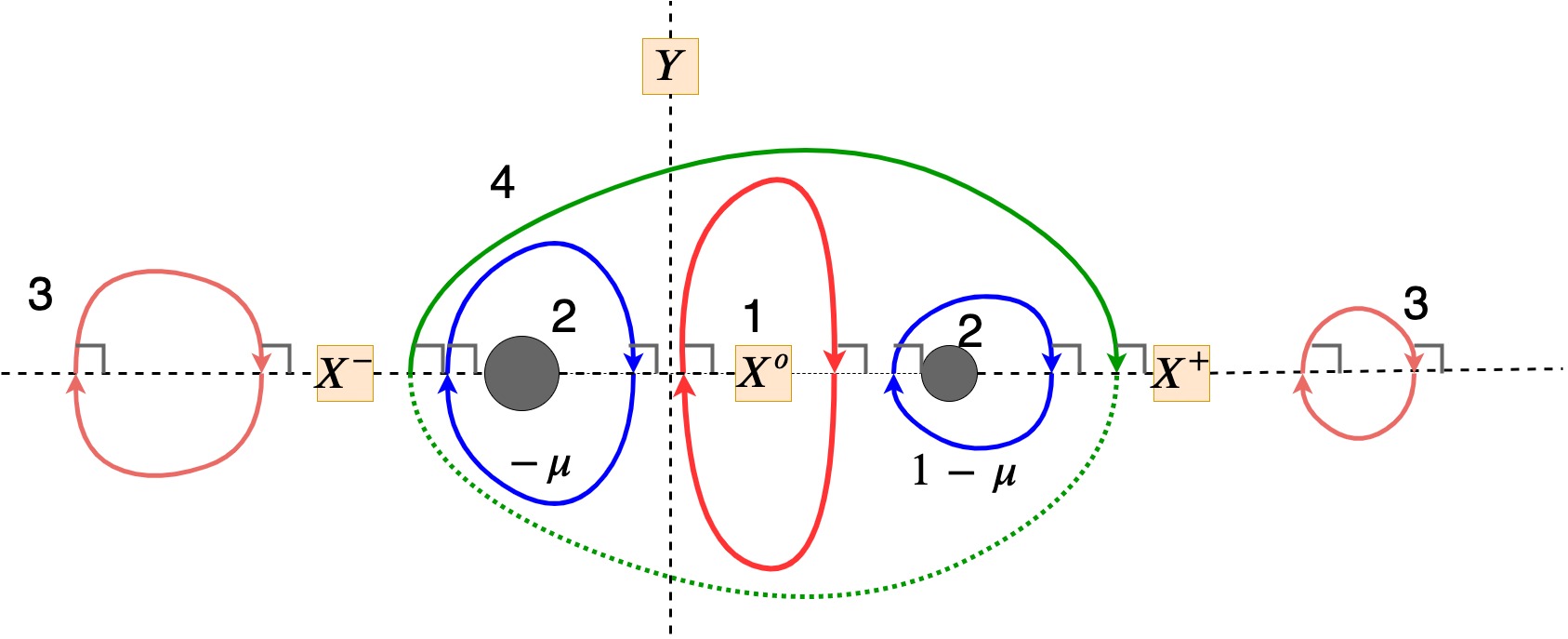
ロケットの軌道設計
| 氏名 | 専攻 | 研究室 | 役職/学年 |
|---|---|---|---|
| 梶原唯加 | 数理工学専攻 | 力学系数理分野 | 博士1回生 |
| 柴山允瑠 | 数理工学専攻 | 力学系数理分野 | 准教授 |